アインシュタインは「複利は人類最大の発明」であると言いました。
“投資の神様”ウォーレン・バフェットも若かりし時から複利の重要性を認識し、大成功を収めました。
数年前に参加した無料投資セミナーで、とある電子書籍をもらいました。
タイトルは
『バフェットと釣りに行く』。
この電子書籍の中にある、複利に関する面白い物語を引用し、投資家であるあなたに複利の大切さを感じて頂きたい、というのがこの記事の目的です。
物語は”おじさん”(バフェットのこと)と26歳の青年・ショーンの会話形式で進んでいきます。
■電子書籍『バフェットと釣りに行く』より(一部抜粋、加筆)

釣りはできるか?

まぁ、学生の頃に釣りはしてましたけど・・・なぜですか?

どうだ、釣りで勝負してみないか?
(中略)

じゃあ賭けをしようか。先に魚を捕まえた方が勝ちだ。敗者は勝者に、そうだな、1セント($0.01)払うのでどうだ。勝負できるか?

1セントですか?まぁ、それなら勝負できますけど、その金額だと楽しくない気もしますが

楽しくない?そうだね。じゃあ、先に捕まえた方が1セントもらえる。そしてここで面白くしよう、2回目の勝負に賭け金をダブルにして、先に魚を捕まえた人が今度は2セント($0.02)もらえる。どうだ、まだ勝負できそうか?

2セントですよ?それくらいは払います。それでも面白くなったように思えませんが。

じゃあ、賭け金をダブルにする勝負を30回やるのはどうだ?それでも勝負できるか?

30回?数ドルくらいになりそうですね。たぶん大丈夫だと思います

本当か?そんなにお金持ちには見えなかったがな。(おじさんはニヤっと微笑み、コカコーラを一口飲んだ。)では、釣りの開始だ。
■複利の力
さて、こうしておじさん(バフェット)と青年の勝負が始まりました。
物語の中で、2人は実際に釣りをするのではなく(そもそも青年は釣竿も持っていない)、頭の中で勝負をします。
皆さんも頭の中で、もしくはペンと紙を用意して、計算しながら続きを読んでみてください。
ゲームに戻ります。

さて、ゲームに戻ろう。さっき30回まで賭ける事ができると言ったな、そこまでの金額を賭けられると確認したことにするぞ。それも何回か私に負けて賭け金を払う事が前提だ。では早速、3回目の賭け金はいくらだ?

えーと、1回目は1セント、2回目は2セントだとすると、3回目は4セント($0.04)です

よし。まだ4セントは払えるよな。もし君が10回目に負けたら私にいくら払う事になるかな?
ショーンはノートに計算を書き出した。
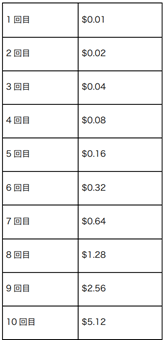

えーと、$5.12になります。大丈夫ですよ、この額ならまだ払えます

おお、そうか。じゃあ、30回目に負けた場合は払えるかな?

問題ないと思いますよ

では、そこに行く前に20回目の掛け金が払えるか計算して確認してもらって良いかな?

もちろん
ショーンはノートの計算を続けた。
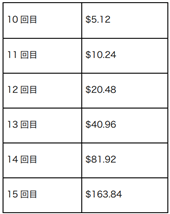

え!15回目で100ドル台に入ってます?!(ショーンは驚きを示した)

100台に?!すごいな、20回目の掛け金はいくらぐらいになるかね。(おじさんは笑みを見せながら無邪気に)
ショーンは計算を続けた。
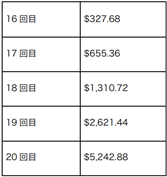

$5,242.88?!(ショーンは息を呑んだ)

まだ20回目だぞ。誰かさんは30回目になっても大丈夫だと言ってたな・・・
ショーンは恥ずかしそうにニコッとしながら、計算を続けた。
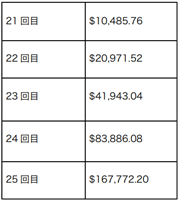
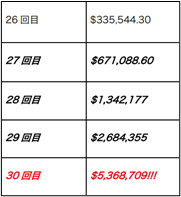

500万ドル!何が起きたんですか?!ちょっと前までは数セントだったのが、数ドルになったのに、どのように100万台に?私は何をしたんですか?(ショーンは衝撃を受けた)

君はね、お金持ちになる方法を見つけたんだよ。
お金をどのように投資してダブルの資金にするかを学べばね。
これは複利効果と言われているんだ。
約60年前に複利効果を知った時、
私の人生は大きく変わったんだ。
■おわりに/72の法則
この物語は、複利の力を伝えるため、大げさに賭け金が倍倍で増える設定になっていますので、ここまで爆発的に資産が増えることは現実的ではありません。
ただ、複利の持つ力はすごい、ということは、十分に伝わる物語だと思います。
今回のゲームの金額の推移をグラフにすると、以下の通りです。
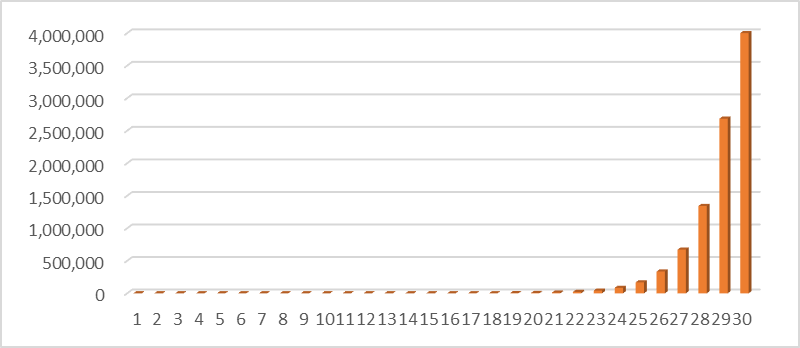
終盤に飛躍的に金額が大きくなっています。(30回目の棒グラフは、途中で切っています。)
これがまさに複利の力です。
「72の法則」という資産運用の世界で有名な法則があります。
「72 ÷ 金利 = お金が2倍になる期間」
という法則です。
例えば、年利6%で資産を運用すると、12年間で資産が倍になる、ということです。
実際に計算してみると・・・
1年後:106万円 (対前年+6万円)
2年後:112.36万円(対前年+6.36万円)
3年後:119.10万円(対前年+6.74万円)
4年後:126.24万円(対前年+7.14万円)
5年後:133.82万円(対前年+7.58万円)
6年後:141.85万円(対前年+8.03万円)
7年後:150.36万円(対前年+8.51万円)
8年後:159.38万円(対前年+9.02万円)
9年後:168.94万円(対前年+9.56万円)
10年後:179.08万円(対前年+10.14万円)
11年後:189.82万円(対前年+10.74万円)
12年後:201.21万円(対前年+11.39万円)
確かに、100万円で始まった資産が12年後に200万円に、資産が倍になっています。
是非電卓をたたいて確認してみて下さい。
米国株の期待リターンは年間5~7%とも言われますので、こちらは現実的な数字です。
注目すべきは、対前年の資産の増加額が、年々増加していくことです。
毎年同じ6%で運用していても、元手がだんだんと大きくなることで、資産の増加ペースが加速していきます。
これがまさに複利の力です。
資産運用を始めてすぐは資産の額も小さく、複利を実感するのは難しいですが、コツコツと長く続けることで、この複利の力を味わえるようになります。
複利ってすごいですね!
いつか私もそれを味わえる日を信じて、コツコツ資産運用に励んでいきます。
共に頑張りましょう!
本日もお読み頂きありがとうございました!
★★私が株式投資において参考にした書籍を以下の記事にまとめています!★★
よろしければご覧ください!



コメント